Alignment methods (Part 1)

Previous class check-up

We are familiar with git/github
- The class notes are in its own repo:
  - git clone to download
  - git pull to update them, or
  - fork and git pull upstream master
We understand the importance of reproducible scripts
- We created a github repo for the class project (remember to add me as collaborator to your repo)

Learn@Home: Sequencing check-up

We understand sequencing technologies
We learned a bit about phyluce as a pipeline for phylogenomics on UCEs and about FastQC for QC of raw reads
We start thinking about data for the class project and start working on QC if needed -> beginning of work from home in your data!

Learning objectives

At the end of today’s session, you

will be able to explain the most widely used algorithms for pairwise sequence alignment (Needleman-Wunsch algorithm)

No pre-class work.

After today, we will assume that 1) we are all comfortable with the terminal and 2) we are all comfortable with git/github. Note that no one needs to memorize anything. You will always have access to the notes and google. If you are still struggling with the terminal and/or git/github, please check out the resources at the end of the Reproducibility notes. Let’s do this short quiz.

What is multiple sequence alignment (MSA)?

Homology is inferred from an input of sequences that are assumed to have an evolutionary relationship: descended from a common ancestor
Intuitively, an MSA method inserts gap characters (-) inside input sequences to produce a set of longer sequences that are all of the same length, such that residues at the same position in different sequences (aligned residues) share some common properties (homology)
MSA is a crucial step since phylogenetic inference methods assume that residue homology relationships are correctly reflected by the input sequences

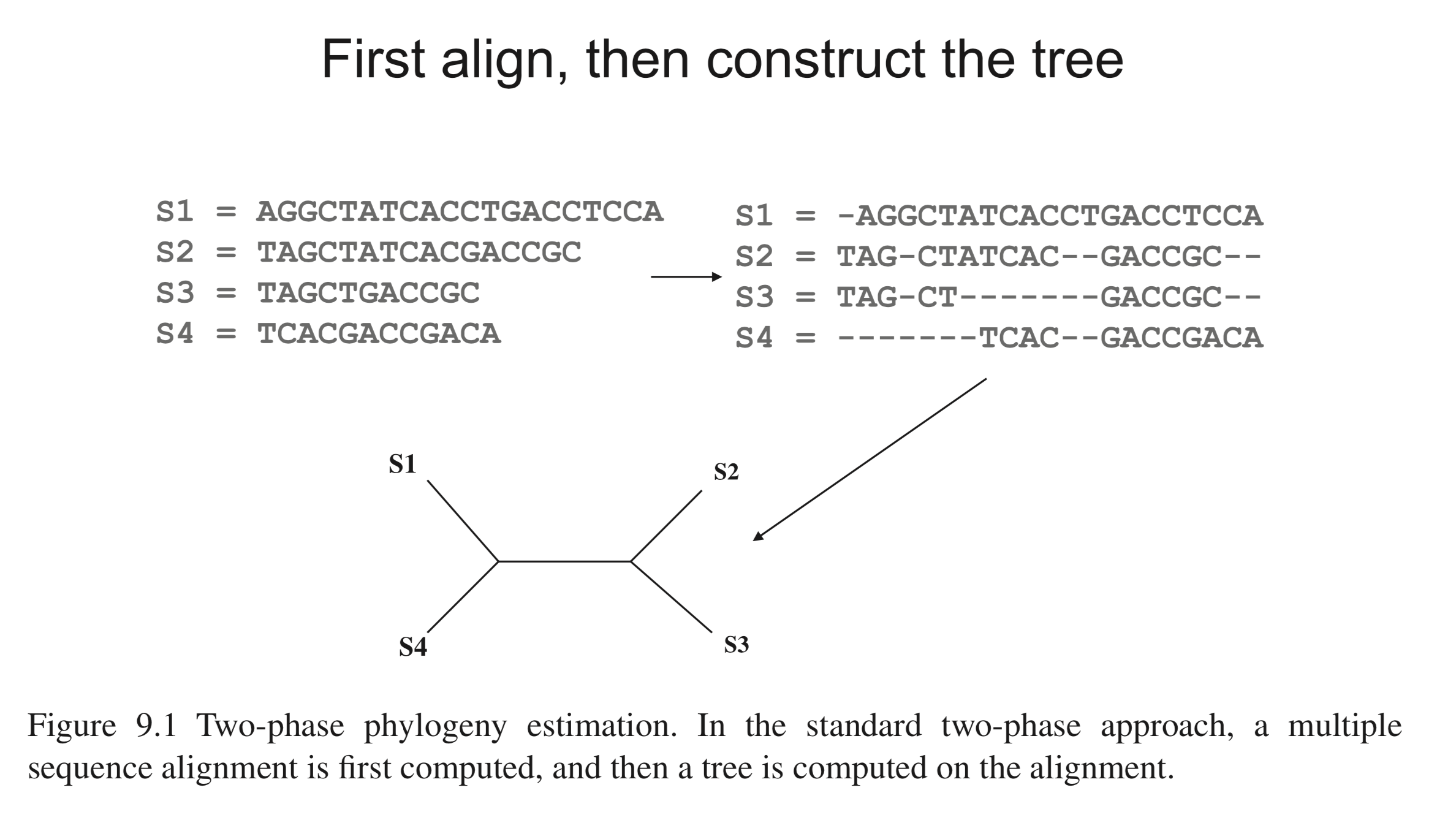
Figure 9.1 in Warnow (2018) Computational phylogenetics

The true MSA reflects the historical substitution, insertion and deletion evolutionary events:

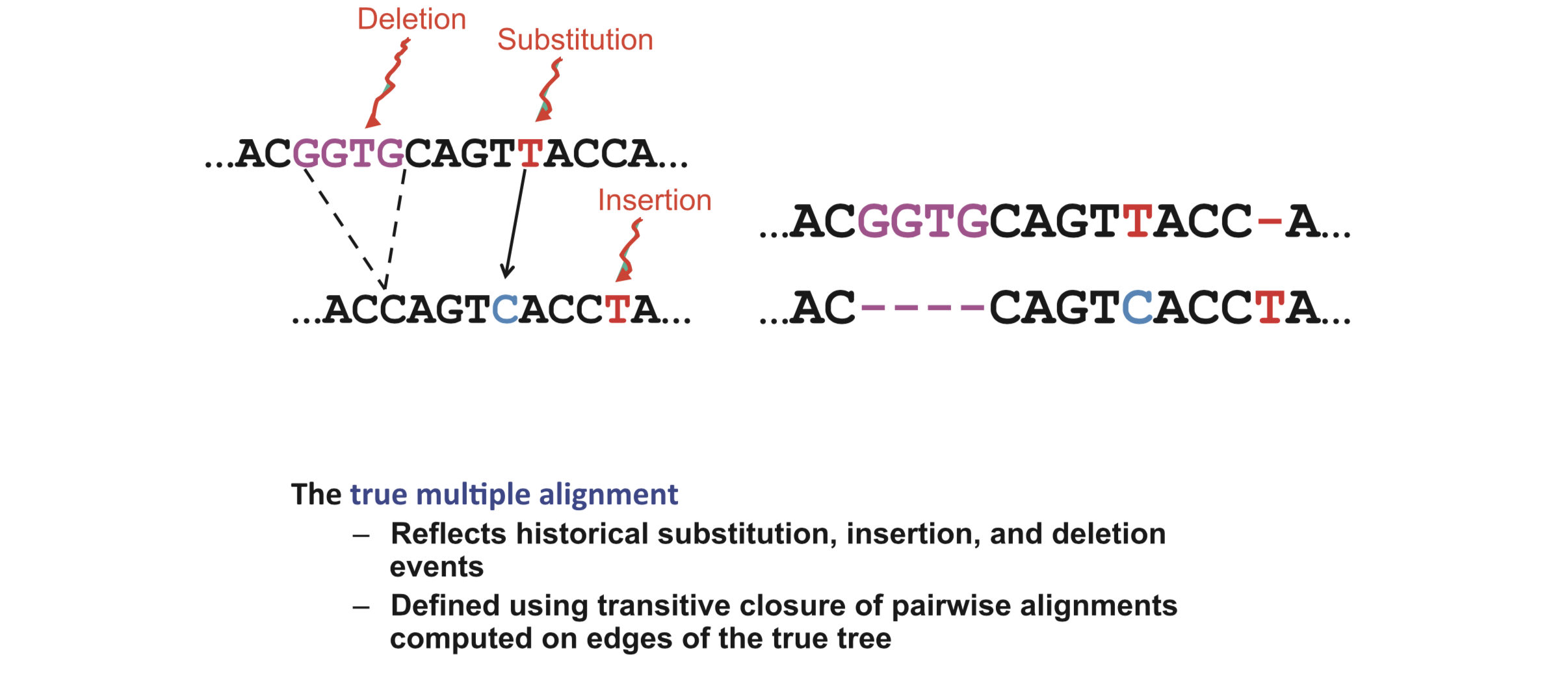
Figure 9.2 in Warnow (2018) Computational phylogenetics

Why is it one of the most computationally intensive tasks? Alignment can be not identifiable or unique.

Example 9.1

Suppose that we knew the true evolutionary events from sequence ACAT to AGAT. Suppose that we knew that it was not a substitution, but a deletion of C (thus creating AAT) followed by an insersion of G. Even in this scenario (when we know the truth), there are two ways to represent the alignment:

AC-AT
A-GAT

and

A-CAT
AG-AT

In-class activities

Table 9.1 (Warnow). What would be the alignment of the sequence S=ACATTA which evolves into S'=TACA if we knew the true evolutionary events?

deletion of the first two nucleotides AC
deletion of the second T
substitution of T into C
insersion of T at the front

Solution: In class.

Table 9.2 (Warnow). Without knowing the true evolutionary events from S=ACATTA to S'=TACA, what would you think is a good alignment?

Solution: You probably choose an alignment where none (or few) of the true homology relationships are correct.

The true alignment has 4 events: 2 deletions, 1 insersion, 1 substitution
The estimated alignment we created now also has 4 events: 3 deletions and 1 insersion
The algorithm will ultimately choose an alignment based on how we penalize each of the events

First key insight for MSA: We are guiding the algorithms by selecting the penalties for evolutionary events: substitutions, deletions, insersions. It has nothing to do with true evolutionary events or true homology.

MSA algorithm

Input: unaligned sequences (different lengths)

Output: aligned sequences (same length) where each site is an assertion of homology

Steps in MSA:

Define cost of each event: deletion, insertion, substitution
Learn to obtain the optimal pairwise alignment with the minimum cost (“edit distance”)
Learn to obtain the optimal multiple sequence alignment: we need to be able to align alignments

1. Cost of evolutionary events

cost of deletion/insersion (cost of gap): 1
cost of substitution: 1

Some software/books will use “weights” instead of costs: weight for match: 5; weight for gap: -1; weight for mismatch (substitution): -1. I prefer to use costs because the idea of negative weights is not intuitive.

In-class activities

Table 9.3 (Warnow). How would you align the sequences S=AACT and S'=CTGG when:

cost of gap: 1
cost of substitution: 3 ?

Table 9.3 (Warnow). How would you change the alignment between sequences S=AACT and S'=CTGG if the costs were:

cost of gap: 4
cost of substitution: 1

Solution: In class.

Other types of costs

There are other ways to measure cost/penalty:

sequence identity: number of identical sites in an alignment divided by the total number of aligned positions
biochemical similarity when assigning costs of substitutions (Figure 3.4 HB 3): PAM weight matrices and BLOSUM62 weight matrices

We will continue to use cost for simplicity.

2. Pairwise sequence alignment

Pairwise alignment of short toy sequences (like in the examples) can be done by hand
Pairwise alignment of real sequences would be too difficult to do by hand, so we need smart algorithms: Needleman-Wunsch algorithm
Needleman-Wunsch is a dynamic programming algorithm
Dynamic programming: optimization algorithm that simplifies a complicated problem by breaking it down into simpler sub-problems in a recursive manner

Needleman-Wunsch algorithm

Ingredients:
- Two sequences: $A=a_1 a_2 ...a_m$ and $B=b_1 b_2 ...b_n$
- 1) cost of gap and 2) cost of substitution
Denote $F(i,j)$ the minimum cost to align sub-sequences $A_i$ and $B_j$ based on the costs

Main principle: When we want to compute $F(i,j)$, we assume that we have already computed all smaller sequences (sub-problems): $F(i-1,j-1), F(i,j-1), F(i-1,j)$.

The final site of the alignment must take one of the following forms:

$a_i$ and $b_j$ are aligned together in the final site. Then the other sites define a pairwise alignment of $A_{i-1}$ and $B_{j-1}$
$a_i$ is aligned with a gap in the final site. Then $A_{i-1}$ and $B_{j}$ defined a pairwise alignment
$b_j$ is aligned with a gap in the final site. Then $A_{i}$ and $B_{j-1}$ defined a pairwise alignment

Example of notation

Let $A=a_1 a_2 a_3 a_4 a_5 a_6$ and $B=b_1 b_2 b_3 b_4 b_5$, and suppose you want to align sites $a_5$ ( $i=5$ ) and $b_3$ ( $j=3$ ). We have three options:

$a_5$ and $b_3$ are aligned together in the final site. Then the other sites define a pairwise alignment of $A_4=a_1 a_2 a_3 a_4$ and $B_2=b_1 b_2$ (we do not know how at this point)
$a_5$ is aligned with a gap in the final site. Then $A_4=a_1 a_2 a_3 a_4$ and $B_3=b_1 b_2 b_3$ define a pairwise alignment
$b_3$ is aligned with a gap in the final site. Then $A_5=a_1 a_2 a_3 a_4 a_5$ and $B_2=b_1 b_2$ define a pairwise alignment

Needleman-Wunsch algorithm: Costs

If $a_i$ and $b_j$ are aligned together in the final site, then the cost is 0 if $a_i=b_j$ and 1 (or whatever cost of substitution defined) if they are different. Hence, the total cost is $F(i,j) = F(i-1,j-1)+cost(a_i,b_j)$
If $a_i$ is aligned with a gap in the final site, then the cost is 1 (or whatever the cost of gap is). Hence, the the total cost is $F(i,j) = F(i-1,j)+1$
If $b_j$ is aligned with a gap in the final site, then the cost is 1 (or whatever the cost of gap is). Hence, the the total cost is $F(i,j) = F(i,j-1)+1$

How to know which of the three options to do? We choose the one with minimum cost!

$F(i,j)=min \{F(i-1,j-1)+cost(a_i,b_j), F(i-1,j)+1, F(i,j-1)+1 \}$.

Needleman-Wunsch algorithm

Compute $F(i,j)$ for every $i,j$ and put in a matrix (sometimes denoted dynamic programming (DP) matrix). First column/row correspond to gap and F(0,0)=0
As you fill the matrix, keep track of which of the three entries gave you the minimum with an arrow
Trace back the arrows to construct the alignment (diagonal arrow=nucleotide, vertical/horizontal arrow=gap replacing the nucleotide the arrow is pointing)

Figure 9.3 from Warnow (2018) Computational phylogenetics

In-class example: We want to align $S_1=ATCG$ and $S_2=TCA$ for a cost of substitution of 1 and cost of gap of 2. We will work through the steps of creating the F matrix in class, and then, as homework, you can complete the whole matrix.

How do we get the alignment after building the F matrix?

We trace back the arrows from the bottom right corner:

ATCG
-TCA

Take-home message: The final alignment depends on the costs of gaps and substitutions.